什么是“胡不归”问题
什么是“胡不归”问题,这是一个悲情的故事:

从前,有一个身在他乡求学的书生,突然得知家乡的老父亲病危,书生便日夜兼程赶路回家。

此时有两条路可走,一条是遍布沙砾的荒漠之地,这样路程是最短的;
另一条路是先走一段驿道,然后再走一段沙砾地也能到家,但这样路程会变长。

大眉山古驿道
但是,沙砾地遍布沙石,荒无人烟,行走困难,而驿道有非常方便的车马道,行走方便。
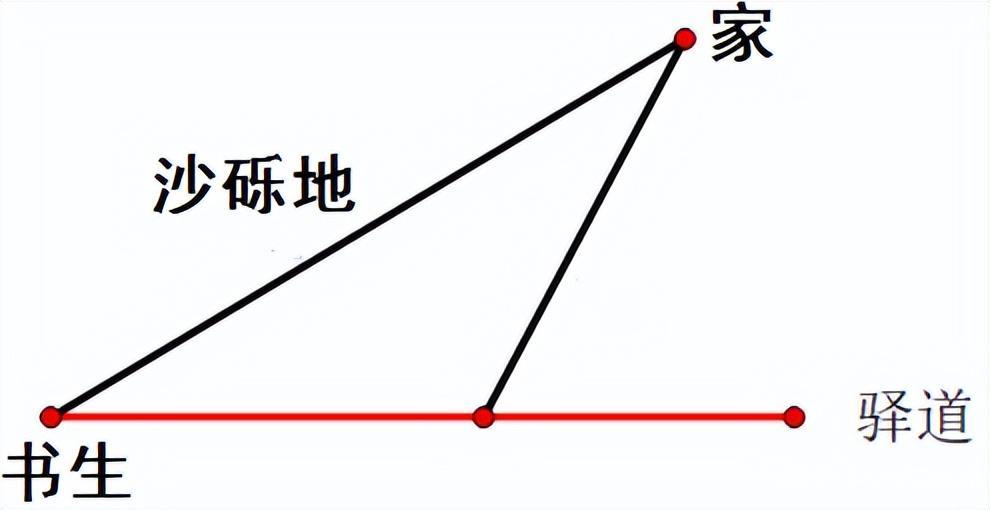
书生心急如焚,最终选择了走沙砾地的直线路径。
然而,当他气喘吁吁地来到父亲的面前时,老人刚刚咽气了。

人们告诉他,在弥留之际,老人在不断喃喃地叨念:“胡不归?胡不归?”。(为何没回来!)

书生非常遗憾,没能见上父亲一面,于是书生悔恨不已,发誓要找到最短的路。
经过学习研究,书生最终找到了这条最省时间的路,只可惜未能见父亲最后一面。
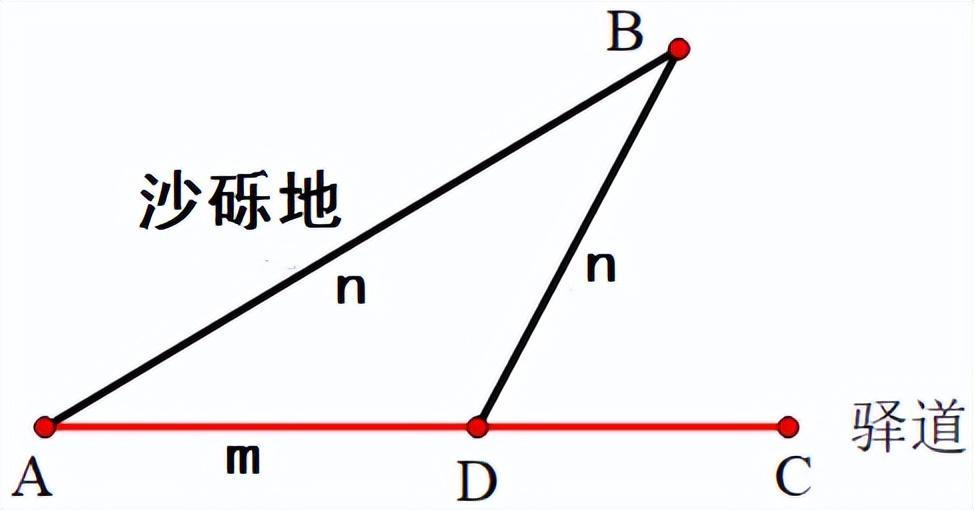
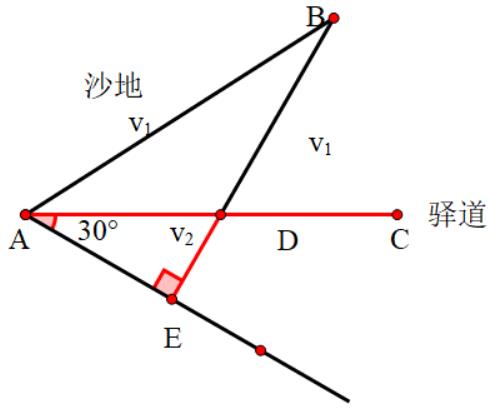
A是出发地,B是目的地,AC是驿道,AC上侧是沙地。为了急切的回家,小伙子选择了AB这条路。但是他忽视了沙地上行走速度慢的问题,即使AB的路程更短,但比走A-D-B路径所花的时间更长。怎么办呢?
设驿道上的速度为m,沙地的速度为n,先假设,驿道上的速度是沙地上速度的2倍,即m=2n,怎样选择才能使行进的时间最短呢?
书生需要在AC上选取一点D,再折往至B。行进时间为,又因为m=2n,即所需时间可变形为,所以问题就转化为求的最小值。
怎样转化呢?看到,可以联想到30度角所对的直角边是斜边的一半,所以可以在AC下侧作一个30度的角,再作DE垂直AE,则DE=,所以只需求BD+DE的最小值。
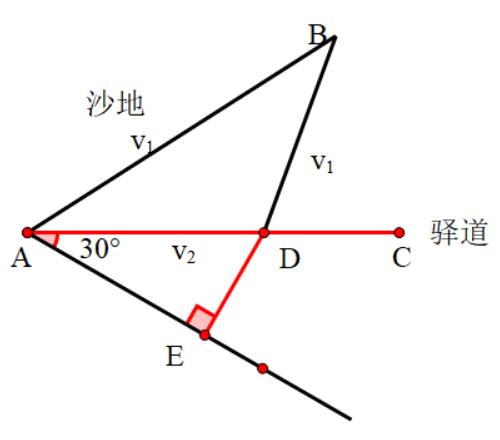
很明显的当B、D、E三点共线时,可取最小值,这样问题就可以顺利解决了.
初中数学中的“PA+PB”型的最值问题,可以运用常见的“将军饮马”模型解决,但当遇到“PA+k·PB”型的最值问题时,再用“将军饮马”模型就无法解决,此时可分为两种类型进行解决:
当P在圆周上运动时,即称为“阿氏圆”问题。(上篇文章已讲到)
当P在直线上运动时,即称为“胡不归”问题;